曉查明敏發自凹非寺

量子位報道公眾號QbitAI

沒想到古代韓信點兵的傳說后來竟然啟發了計算機加密算法

相傳楚漢爭霸之時韓信率1500名將士與楚軍交戰敗退退往山上這時候敵軍率五百騎殺奔而來韓信便急速點兵迎敵

韓信命令士兵3人一排結果多出2名接著命令士兵5人一排結果多出3名他又命令士兵7人一排結果又多出2名

韓信馬上算出軍中還剩1073人而敵人不足五百而且居高臨下以眾擊寡于是率軍殺得敵方大敗而逃

韓信是如何算出人數的背后的算法又是如何影響當今的計算機領域且往下看

韓信還是個數學家

當然韓信算出士兵人數只是個傳說韓信本人并非數學大師這個問題最早見于一本1700年前的古籍已經是韓信死后600多年了

在

南北朝

時期

孫子算經

記述了這樣一個問題注這位孫子不是寫孫子兵法的孫武

原書是這樣說的

有物不知其數三三數之剩二五五數之剩三七七數之剩二問物幾何

意思是一個整數除以三余二除以五余三除以七余二求這個整數

它就是

中國剩余定理

也被叫做韓信點兵問題

在近代數學中很少有以中國數學家命名的重要定理然而這樣一條數學定理名字里就有中國二字

南宋時期我國數學家秦九韶首先給出了這類問題的解法

大衍術

直到500年后著名數學家高斯才在自己的書中描述類似的結果

那么問題來了傳說中的韓信到底是怎么算出來人數的呢

韓信點兵問題求解

為了更好地理解和表述韓信點兵問題我們引入一個新的數學概念同余

在數學上如果a和b除以正整數m后的余數相同

則稱ab對于模m同余

韓信點兵用數學公式來表示就是X是未知的人數

X2mod3X3mod5X2mod7

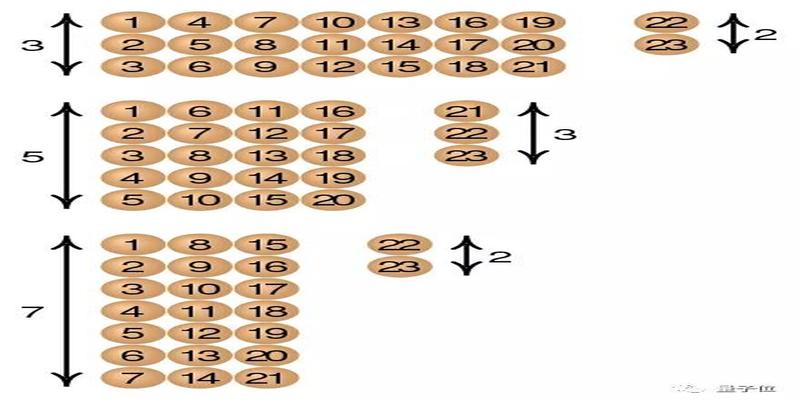
為了簡化問題我們先只考慮前兩個同余條件滿足除以3余2除以5余3的整數分別為

25811141720232638131823283338

可以看出同時符合這兩個條件的第一個數是

8

第二個數是

23

后面的每個解與前一個之差都應該是3和5的最小公倍數

15

即

X815KK是整數

這樣我們就把尋找的整數解縮小了接著再加入第三個條件找到分別滿足X815K和除以7余2的數

823385368839811312829162330374451

滿足條件的第一個數是23第二個數是128后面的每個解與前一個之差都應該是357的最小公倍數105

這樣尋找解的過程顯然太繁瑣后來明朝數學家程大位把求解方法編成了一首詩

三人同行七十稀五樹梅花廿一枝

七子團圓正半月除百零五便得知

意思是

將除以3得到的余數乘以70將除以5得到的余數乘以21將除以7得到的余數乘以15全部加起來后再減去105或者105的整數倍得到的數就是答案

702213152233210523

其他的解只能和23相差105的整數倍韓信應該是估計出軍隊大致人數取了10510231073這個解

以上702115幾組數到底是怎么來的有興趣的讀者可以進一步閱讀中國剩余定理的通解在此不再贅述

這道韓信點兵問題不僅僅能用于點兵甚至在天文歷法上也有重要應用

假設有一顆彗星4年出現一次我們在1991年看到了它另一顆彗星10年看到一次我們在1997年看到了它我們下一次在同一年看到它們是什么時候

X1991mod4X1997mod10

經過計算它們上一次相會是在2007年而且每隔20年重逢一次所以下一次應該是2027年

時至今日中國剩余定理已經成為了很多計算機加密算法的基礎它的應用范圍已經超乎你的想象

影響當今計算機算法

外媒Quantamagazine在一篇名為

古代戰爭計策是如何影響當代數學

的文章中也提到中國剩余定理對現代數學計算機算法天文學等領域都有很大的啟發意義

比如非常有名的

RSA加密算法

就應用了中國剩余定理

我們知道在數論中想要求解出兩個大素數比較簡單但是想要對它們的乘積進行因式分解就很困難了

而RSA加密算法就是把這個乘積作為了自己的加密密鑰

從1977年誕生以來RSA加密算法已經成為了應用最廣泛的公鑰算法之一

此外在

快速傅里葉變換

FFT

中也應用了中國剩余定理它可以大大減少計算離散傅里葉變換時所需的乘法次數

這幾年中國剩余定理還被用到了

信息加密

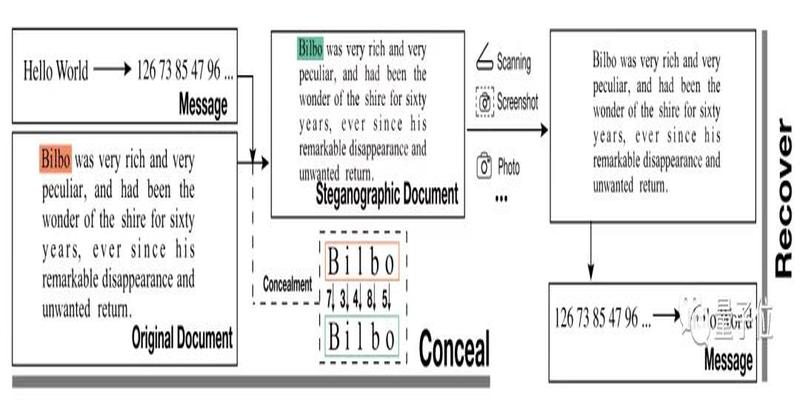
上

2018年哥倫比亞大學的學者們發明了一種可以

在文本中加密信息

的方法其中就應用了中國剩余定理來確保信息復原時的準確性

只要手機對著一段文字掃一掃算法就能給出加密后的信息

這種方法名叫

FontCode

它是對普通字符進行微小的調整然后再對調整后的字符重新編碼信息從而實現對信息的加密

比如以下5種不同顏色的a它們分別代表了15的數字信息

如果不用顏色區分肉眼很難分辨出它們和常規字體之間有什么不同

但是機器可以

只要通過掃描和分析算法就能推斷出哪些字母被特殊處理過處理后的字母又表示了什么信息

因此在一段看似普通的文本中可以很好隱藏這些特殊的字母從而傳遞出一段加密的

數字串

然后再對這些數字進行計算就能得出真實想要傳遞的信息

但是這樣的加密方式還不夠保險畢竟字符出現在屏幕或紙面上時它的格式都有可能發生一些細小的變化

這時就需要

中國剩余定理

登場了

在上面我們已經介紹了通過線性同余方程組就能計算出數值

如果想求解3個未知量那么需要3個線性方程才能做到

現在為了保險起見科學家們把線性方程的數量增加了

比如為了求解出3個未知量他們會設置5個線性方程5個方程中只要知道3個就能求解出想要的答案了

顯然1000多年過去了雖然我們不會再像韓信點兵一樣隱藏士兵數量但是現代數學計算機等領域的研究者們依舊能從中國剩余定理中獲得源源不斷的啟發

參考鏈接1完

量子位QbitAI頭條號簽約

關注我們第一時間獲知前沿科技動態