世紀(jì)難題黎曼猜想已經(jīng)被證明？

英國著名數(shù)學(xué)家阿蒂亞（Michael Atiyah）將在9月24日在海德堡獲獎?wù)哒搲难葜v中公布他對黎曼猜想的證明。阿蒂亞表示，他是基于馮·諾依曼、希策布魯赫和狄拉克等人的成果，使用一種簡單而全新的方法證明了黎曼猜想的。

2018年會成為載入數(shù)學(xué)史的一年嗎？也許我們真的有這樣的機(jī)會，而答案將在9月24日揭曉。

四年一屆的國際數(shù)學(xué)家大會剛剛于今年8月在巴西召開并頒發(fā)了數(shù)學(xué)界最重要的獎項之一的菲爾茲獎，因此2018年原本對國際數(shù)學(xué)界而言就算是一個“大年”，這有些類似于同樣在今年舉辦的俄羅斯世界杯對足球的意義。但是，就在大家覺得數(shù)學(xué)熱潮已過并將目光轉(zhuǎn)向即將公布的諾貝爾獎的時候，一條簡短的新聞令眾人的目光重新投向數(shù)學(xué)界——英國著名數(shù)學(xué)家邁克爾·阿蒂亞爵士（Michael Atiyah）將在9月24日于海德堡獲獎?wù)哒搲℉eidelberg Laureate Forum）的演講中公布他對黎曼猜想的證明。

邁克爾·阿蒂亞（海德堡獲獎?wù)哒搲俜骄W(wǎng)站截圖/圖）

海德堡獲獎?wù)哒搲瘎?chuàng)辦于2013年，舉辦地是德國海德堡，每年舉辦一次，今年是第六屆。這個論壇參照創(chuàng)立于1951年的林道會議（Lindau Meetings），希望提供一個數(shù)學(xué)及計算機(jī)科學(xué)大師與年輕科學(xué)家面對面交流的機(jī)會。今年的會議可謂大師云集，與會者包括十幾位曾經(jīng)獲得過菲爾茲獎和計算機(jī)科學(xué)領(lǐng)域最高獎項圖靈獎的著名學(xué)者，其中就包括阿蒂亞。

阿蒂亞出生于1929年，現(xiàn)年89歲。他在數(shù)學(xué)的多個領(lǐng)域做出過杰出貢獻(xiàn)，證明了阿蒂亞-辛格指標(biāo)定理，曾先后獲得過菲爾茲獎（1966年）和阿貝爾獎（2004年），并曾于1990年至1995年擔(dān)任英國皇家學(xué)會主席，是當(dāng)代最偉大的數(shù)學(xué)家之一。

這場被安排在德國當(dāng)?shù)貢r間9月24日上午9：45-10：30的演講因為阿蒂亞將公布對黎曼猜想的證明而引起全世界的關(guān)注。這樣的關(guān)注，正是源自黎曼猜想在數(shù)學(xué)中舉足輕重的意義。

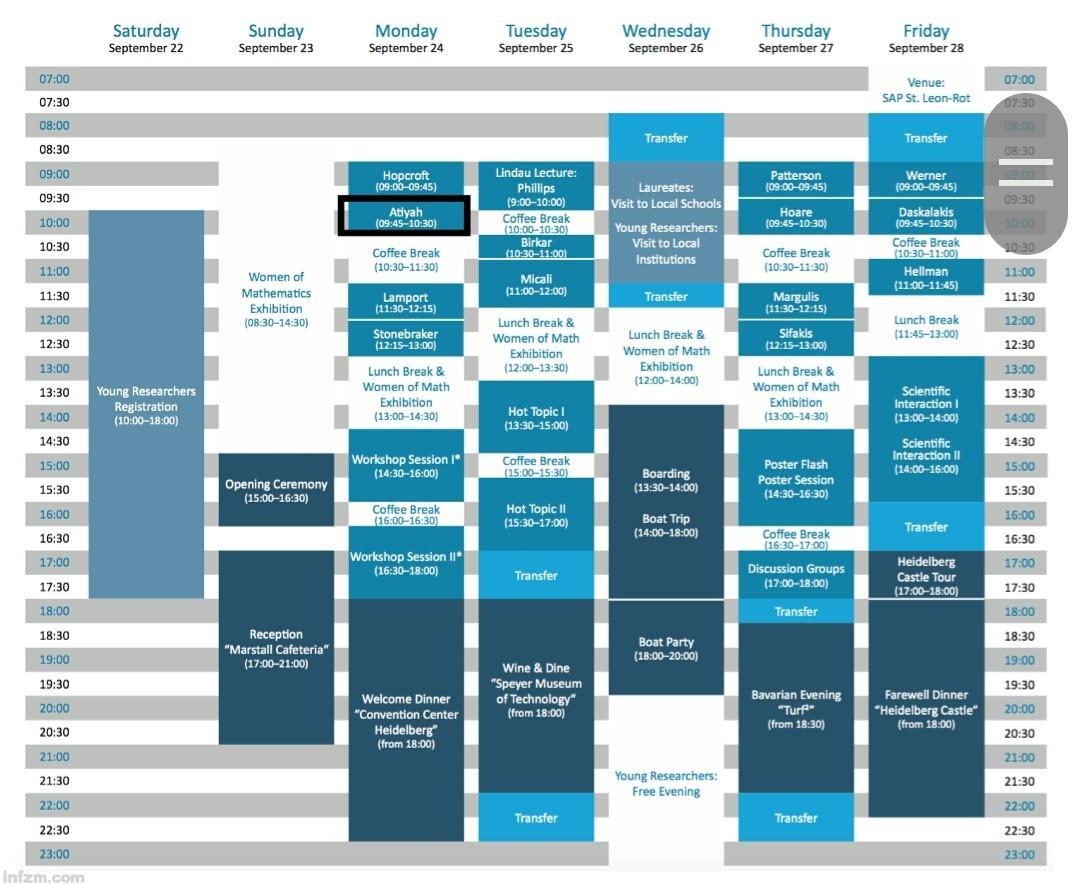
2018年海德堡獲獎?wù)哒搲粘蹋诳驑?biāo)出的是阿蒂亞的演講時間（海德堡獲獎?wù)哒搲俜骄W(wǎng)站截圖/圖）

黎曼猜想以德國著名數(shù)學(xué)家波恩哈德·黎曼（Bernhard Riemann）的名字命名。1859年，他在一篇研究黎曼澤塔函數(shù)（Riemannzetafunction）的論文中提出了這個猜想。這個函數(shù)是一個復(fù)變量函數(shù)，就是變量和函數(shù)值都在復(fù)數(shù)域中取值的函數(shù)。簡單地說，這個函數(shù)會在某些點上取值為0，而在這些點中，有些被稱作是非平凡0點。黎曼在研究中發(fā)現(xiàn)，這些非平凡0點都分布在一條特殊的直線上，這條直線通過實軸上的點（1/2，0）并和虛軸平行，也就是說，這些非平凡0點的實數(shù)部分都是1/2。

波恩哈德·黎曼（維基百科/圖）

黎曼提出這個想法后并沒有給出證明，這個想法也就停留在“猜想”階段。從那時起，黎曼猜想就成為困擾數(shù)學(xué)界的難題，以至于在20世紀(jì)和21世紀(jì)這兩個世紀(jì)開始的時候都被標(biāo)記為“世紀(jì)難題”。

1900年，偉大的數(shù)學(xué)家大衛(wèi)·希爾伯特（David Hilbert）在巴黎的國際數(shù)學(xué)家大會上提出了23個未解決的重要數(shù)學(xué)問題。這些問題中有些在隨后很短的時間內(nèi)就得到解決，但有的問題卻異常復(fù)雜，影響貫穿整個20世紀(jì)的數(shù)學(xué)研究，窮盡數(shù)學(xué)家一個世紀(jì)的努力都沒有被解決，黎曼猜想就在其中。

2000年，美國克雷數(shù)學(xué)研究所公布了一個包含7個尚未被解決的數(shù)學(xué)問題的“千禧年大獎難題”清單，成功解決其中任何一個問題的數(shù)學(xué)家都將獲得100萬美元的獎金。但是，迄今為止，7個問題中只有龐加萊猜想在2003年被俄羅斯數(shù)學(xué)家格里高利·佩雷爾曼（Grigori Perelman）解決，他也因此在2006年獲得了菲爾茲獎。其余6個問題目前仍懸而未決，其中還包括黎曼猜想。

即使使用非常簡化的語言來描述，黎曼猜想對沒有一定數(shù)學(xué)基礎(chǔ)的讀者來說仍然不易理解。但是從這個猜想兩次被列入“世紀(jì)難題”的范疇卻仍然是“猜想”的事實，就不難想到它對數(shù)學(xué)家提出的挑戰(zhàn)有多么嚴(yán)峻。

不過，雖然黎曼猜想并沒有被證明，卻不妨礙數(shù)學(xué)家使用黎曼的發(fā)現(xiàn)。目前已經(jīng)有超過1000個數(shù)學(xué)命題是以黎曼猜想或者它的推廣形式為基礎(chǔ)，也就是說數(shù)學(xué)家在提出這些命題的時候，已經(jīng)假定黎曼猜想成立。由此可見，黎曼猜想的證明也將最終夯實這些命題存在的根基。

此外，從更大的視野上來看，在解決一些重要數(shù)學(xué)問題的過程中，數(shù)學(xué)家會提出一些新的數(shù)學(xué)方法。這些方法將會豐富數(shù)學(xué)家的研究手段，促進(jìn)其他數(shù)學(xué)問題的解決，英國數(shù)學(xué)家安德魯·懷爾斯（Andrew Wiles）解決費馬大定理就是這樣一個例子。而在將近160年的歷史上，數(shù)學(xué)家在嘗試證明黎曼猜想的過程中，也取得了類似的收獲。

阿蒂亞表示，他基于馮諾依曼（von Neumann）、希策布魯赫（Hirzebruch）和狄拉克（Dirac）等人的研究成果，使用一種全新的方法對黎曼猜想給出一個簡單的證明。在演講開始之前，外界對這個證明的細(xì)節(jié)不得而知，所以究竟方法是如何“全新”、證明是怎樣“簡單”，我們只能拭目以待。

阿蒂亞（左）與希策布魯赫（右）（維基百科/圖）